树必刷题第一部分

144. 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

解题思路

遵循以下顺序：根节点 -> 左子树 -> 右子树。步骤如下：

1. 首先，初始化一个空列表 result，用于存储遍历过程中的节点值。
2. 确保根节点 root 不为 None，因为一个空树没有节点可以遍历。
3. 遍历过程可以通过递归或迭代的方式实现。我们将分别介绍这两种方法。

解法一：递归方法

1. 从根节点开始遍历。
2. 将当前节点值添加到 result 列表中。
3. 如果当前节点有左子节点，递归遍历左子树。
4. 如果当前节点有右子节点，递归遍历右子树。
5. 当遍历完成后，返回 result 列表。

解法二：迭代方法

1. 初始化一个空栈 stack，用于辅助遍历。
2. 将根节点压入 stack。
3. 当 stack 非空时，重复以下步骤： a. 弹出 stack 顶部的节点，并将其值添加到 result 列表中。 b. 如果该节点有右子节点，将右子节点压入 stack。 c. 如果该节点有左子节点，将左子节点压入 stack。
4. 当遍历完成后，返回 result 列表。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
// 递归
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        preorder(root, result);
        return result;
    }
    
    void preorder(TreeNode* node, vector<int>& result) {
        if (!node) return;
        result.push_back(node->val);
        preorder(node->left, result);
        preorder(node->right, result);
    }
};

// 迭代
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        if (!root) return result;
        stack<TreeNode*> stack;
        stack.push(root);
        while (!stack.empty()) {
            TreeNode* node = stack.top();
            stack.pop();
            result.push_back(node->val);
            if (node->right) stack.push(node->right);
            if (node->left) stack.push(node->left);
        }
        return result;
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
// 递归
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        preorder(root, result);
        return result;
    }
    
    private void preorder(TreeNode node, List<Integer> result) {
        if (node == null) return;
        result.add(node.val);
        preorder(node.left, result);
        preorder(node.right, result);
    }
}
// 迭代
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
        }
        return result;
    }
}

// 递归
func preorderTraversal(root *TreeNode) []int {
    result := []int{}
    preorder(root, &result)
    return result
}

func preorder(node *TreeNode, result *[]int) {
    if node == nil {
        return
    }
    *result = append(*result, node.Val)
    preorder(node.Left, result)
    preorder(node.Right, result)
}

// 迭代
func preorderTraversal(root *TreeNode) []int {
    result := []int{}
    if root == nil {
        return result
    }
    stack := []*TreeNode{root}
    for len(stack) > 0 {
        node := stack[len(stack) - 1]
        stack = stack[:len(stack) - 1]
        result = append(result, node.Val)
        if node.Right != nil {
            stack = append(stack, node.Right)
        }
        if node.Left != nil {
            stack = append(stack, node.Left)
        }
    }
    return result
}

---

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的 中序 遍历 。

解题思路

遵循左子树-根节点-右子树的顺序，下面将从递归和迭代两种思路来说明：

解题思路一：递归法

• 在递归方法中，首先判断根节点是否为空。若为空，则返回空列表。
• 然后分别对左子树和右子树进行递归调用，最后将结果按照左子树-根节点-右子树的顺序进行拼接。

解题思路二：迭代法

• 在迭代方法中，使用一个栈来辅助存储节点。
• 首先，将当前节点和其所有左子节点入栈，然后弹出栈顶元素（当前最左节点），将其值添加到结果列表中，并将当前节点设置为右子节点。
• 继续循环直至当前节点和栈均为空。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 递归
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        inorder(root, result);
        return result;
    }
    
    void inorder(TreeNode* node, vector<int>& result) {
        if (!node) return;
        inorder(node->left, result);
        result.push_back(node->val);
        inorder(node->right, result);
    }
};

// 迭代
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        if (!root) return result;
        stack<TreeNode*> stack;
        TreeNode* curr = root;
        while (curr || !stack.empty()) {
            while (curr) {
                stack.push(curr);
                curr = curr->left;
            }
            curr = stack.top();
            stack.pop();
            result.push_back(curr->val);
            curr = curr->right;
        }
        return result;
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
// 递归
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inorder(root, result);
        return result;
    }
    
    private void inorder(TreeNode node, List<Integer> result) {
        if (node == null) return;
        inorder(node.left, result);
        result.add(node.val);
        inorder(node.right, result);
    }
}

// 迭代
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (curr != null || !stack.isEmpty()) {
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            curr = stack.pop();
            result.add(curr.val);
            curr = curr.right;
        }
        return result;
    }
}

// 递归
func inorderTraversal(root *TreeNode) []int {
    result := []int{}
    inorder(root, &result)
    return result
}

func inorder(node *TreeNode, result *[]int) {
    if node == nil {
        return
    }
    inorder(node.Left, result)
    *result = append(*result, node.Val)
    inorder(node.Right, result)
}

// 迭代
func inorderTraversal(root *TreeNode) []int {
    result := []int{}
    if root == nil {
        return result
    }
    stack := []*TreeNode{}
    curr := root
    for curr != nil || len(stack) > 0 {
        for curr != nil {
            stack = append(stack, curr)
            curr = curr.Left
        }
        curr = stack[len(stack) - 1]
        stack = stack[:len(stack) - 1]
        result = append(result, curr.Val)
        curr = curr.Right
    }
    return result
}

---

145. 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

解题思路

遵循左子树-右子树-根节点的顺序。将从递归和迭代两种思路来说明：

解题思路一：迭代法

• 在迭代方法中，使用一个栈来辅助存储节点。
• 首先，将根节点入栈。然后在循环中，弹出栈顶元素，将其值插入到结果列表的开头。接着按照左子节点、右子节点的顺序将非空子节点入栈。
• 继续循环直至栈为空，最后全部pop出来，得到结果。

解题思路二：递归法

• 在递归方法中，首先判断根节点是否为空。
• 若为空，则返回空列表。然后分别对左子树和右子树进行递归调用，最后将结果按照左子树-根节点-右子树的顺序进行拼接。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
// 递归
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        postorder(root, result);
        return result;
    }
    
    void postorder(TreeNode* node, vector<int>& result) {
        if (!node) return;
        postorder(node->left, result);
        postorder(node->right, result);
        result.push_back(node->val);
    }
};
// 迭代
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        if (!root) return result;
        stack<TreeNode*> stack;
        stack.push(root);
        while (!stack.empty()) {
            TreeNode* node = stack.top();
            stack.pop();
            result.insert(result.begin(), node->val);
            if (node->left) stack.push(node->left);
            if (node->right) stack.push(node->right);
        }
        return result;
    }
};

// 递归
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        postorder(root, result);
        return result;
    }
    
    private void postorder(TreeNode node, List<Integer> result) {
        if (node == null) return;
        postorder(node.left, result);
        postorder(node.right, result);
        result.add(node.val);
    }
}
// 迭代
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(0, node.val);
            if (node.left != null) stack.push(node.left);
            if (node.right != null) stack.push(node.right);
        }
        return result;
    }
}

// 递归
func postorderTraversal(root *TreeNode) []int {
    result := []int{}
    postorder(root, &result)
    return result
}

func postorder(node *TreeNode, result *[]int) {
    if node == nil {
        return
    }
    postorder(node.Left, result)
    postorder(node.Right, result)
    *result = append(*result, node.Val)
}
// 迭代
func postorderTraversal(root *TreeNode) []int {
    result := []int{}
    if root == nil {
        return result
    }
    stack := []*TreeNode{root}
    for len(stack) > 0 {
        node := stack[len(stack) - 1]
        stack = stack[:len(stack) - 1]
        result = append([]int{node.Val}, result...)
        if node.Left != nil {
            stack = append(stack, node.Left)
        }
        if node.Right != nil {
            stack = append(stack, node.Right)
        }
    }
    return result
}

102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

解题思路

层序遍历一般都用迭代来处理：

1. 定义一个双端队列 q，将根节点 root 入队。同时定义一个当前节点指针 cur，一个临时数组 tmp，以及一个结果数组 ans。

2. 判断根节点是否为空。如果根节点为空，说明树为空，直接返回结果数组 ans。

3. 进入循环，当队列不为空时，执行以下步骤：

   a. 获取当前队列的大小 sz，这表示当前层的节点数量。

   b. 清空临时数组 tmp。

   c. 遍历当前层的所有节点，执行以下操作：

   • 从队列头部取出节点（队首），将其值添加到临时数组 tmp 中。
   • 如果当前节点的左子节点不为空，将左子节点加入队列尾部（队尾）。
   • 如果当前节点的右子节点不为空，将右子节点加入队列尾部（队尾）。

   d. 将临时数组 tmp 添加到结果数组 ans 中。

4. 循环结束后，返回结果数组 ans。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
// 迭代
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        if (!root) return ans;
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int sz = q.size();
            vector<int> tmp;
            while (sz--) {
                TreeNode* cur = q.front();
                q.pop();
                tmp.push_back(cur->val);
                if (cur->left) q.push(cur->left);
                if (cur->right) q.push(cur->right);
            }
            ans.push_back(tmp);
        }
        return ans;
    }
};

// 递归
class Solution {
public:
    vector<vector<int>> res;
    vector<vector<int>> levelOrder(TreeNode* root) {
        res.clear();
        dfs(root, 0);
        return res;
    }
    void dfs(TreeNode* root, int level) {
        if (root) {
            if (res.size() == level) {
                res.push_back({});
            }
            res[level].push_back(root->val);
            dfs(root->left, level + 1);
            dfs(root->right, level + 1);
        }
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
// 迭代
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ans = new ArrayList<>();
        if (root == null) return ans;
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {
            int sz = q.size();
            List<Integer> tmp = new ArrayList<>();
            while (sz-- > 0) {
                TreeNode cur = q.poll();
                tmp.add(cur.val);
                if (cur.left != null) q.offer(cur.left);
                if (cur.right != null) q.offer(cur.right);
            }
            ans.add(tmp);
        }
        return ans;
    }
}

// 递归
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        res.clear();
        dfs(root, 0);
        return res;
    }
    void dfs(TreeNode root, int level) {
        if (root != null) {
            if (res.size() == level) {
                res.add(new ArrayList<>());
            }
            res.get(level).add(root.val);
            dfs(root.left, level + 1);
            dfs(root.right, level + 1);
        }
    }
}

// 迭代
func levelOrder(root *TreeNode) [][]int {
    ans := [][]int{}
    if root == nil {
        return ans
    }
    q := []*TreeNode{root}
    for len(q) > 0 {
        sz := len(q)
        tmp := []int{}
        for i := 0; i < sz; i++ {
            cur := q[i]
            tmp = append(tmp, cur.Val)
            if cur.Left != nil {
                q = append(q, cur.Left)
            }
            if cur.Right != nil {
                q = append(q, cur.Right)
            }
        }
        q = q[sz:]
        ans = append(ans, tmp)
    }
    return ans
}

// 递归
var res [][]int
func levelOrder(root *TreeNode) [][]int {
    res = [][]int{}
    dfs(root,0)
    return res
}
func dfs(root *TreeNode,level int){
    if root!=nil{
        if len(res)==level{
            res = append(res,[]int{})
        }
        res[level] = append(res[level],root.Val)
        dfs(root.Left,level+1)
        dfs(root.Right,level+1)
    }
}

662. 二叉树最大宽度

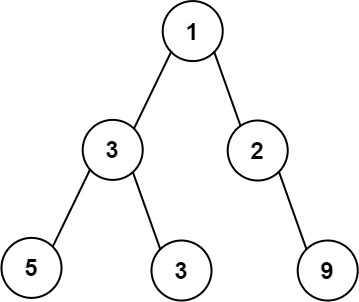
给你一棵二叉树的根节点 root ，返回树的最大宽度 。树的最大宽度是所有层中最大的宽度 。

每一层的宽度被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

解题思路

这道题用层序遍历来处理，对于二叉树可以给每个节点编号，根节点就是1，左子节点就是2 * idx - 1，右子节点就是2 * idx；然后层序遍历搞清楚每一层的最左边和最右边编号，就可以得到宽度。具体解题思路如下：

1. 定义一个 pair<TreeNode*, unsigned long long> 类型的别名 pti，用于存储节点及其位置信息。

2. 若根节点为空，二叉树的最大宽度为 0。

3. 创建一个双端队列 q，将根节点及其位置（1）作为一个 pti 对象加入队列。定义一个变量 ans 存储最大宽度。

4. 进入循环，当队列不为空时，执行以下步骤：

   a. 获取当前队列的大小 sz，表示当前层的节点数量。

   b. 更新最大宽度 ans：取当前层最右侧节点位置与最左侧节点位置之差再加 1，与当前最大宽度取较大者。

   c. 遍历当前层的所有节点，执行以下操作：

   • 取出队首节点及其位置信息。
   • 若当前节点的左子节点不为空，将左子节点及其位置信息（当前节点位置的 2 倍减 1）加入队列。
   • 若当前节点的右子节点不为空，将右子节点及其位置信息（当前节点位置的 2 倍）加入队列。

5. 循环结束后，返回最大宽度 ans。

注意：编号用unsigned long long来存，不然有些用例过不了。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        if (!root) return 0;
        int ans = 0;
        queue<pair<TreeNode*, unsigned long long>> q;
        q.push({root, 1});
        while (!q.empty()) {
            int sz = q.size();
            unsigned long long left = q.front().second, right = left;
            for (int i = 0; i < sz; i++) {
                pair<TreeNode*, unsigned long long> p = q.front();
                q.pop();
                right = p.second;
                TreeNode* node = p.first;
                if (node->left) q.push({node->left, 2 * right});
                if (node->right) q.push({node->right, 2 * right + 1});
            }
            ans = max(ans, (int)(right - left + 1));
        }
        return ans;
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        if (root == null) return 0;
        int ans = 0;
        Deque<Pair<TreeNode, Integer>> q = new LinkedList<>();
        q.offer(new Pair<>(root, 1));
        while (!q.isEmpty()) {
            int sz = q.size();
            int left = q.peek().getValue();
            int right = left;
            for (int i = 0; i < sz; i++) {
                Pair<TreeNode, Integer> p = q.poll();
                right = p.getValue();
                TreeNode node = p.getKey();
                if (node.left != null) q.offer(new Pair<>(node.left, 2 * right - 1));
                if (node.right != null) q.offer(new Pair<>(node.right, 2 * right));
            }
            ans = Math.max(ans, right - left + 1);
        }
        return ans;
    }
}

type pair struct {
    node  *TreeNode
    index int
}

func widthOfBinaryTree(root *TreeNode) int {
    if root == nil {
        return 0
    }
    ans := 0
    q := []pair{{root, 1}}
    for len(q) > 0 {
        sz := len(q)
        left := q[0].index
        right := left
        for i := 0; i < sz; i++ {
            p := q[0]
            q = q[1:]
            right = p.index
            node := p.node
            if node.Left != nil {
                q = append(q, pair{node.Left, 2 * right})
            }
            if node.Right != nil {
                q = append(q, pair{node.Right, 2 * right + 1})
            }
        }
        ans = max(ans, int(right-left+1))
    }
    return ans
}


func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

101. 对称二叉树

给你一个二叉树的根节点root， 检查它是否轴对称。

解题思路

这道题节点数量少，可以直接拿递归做。具体操作如下：

1. 定义一个辅助函数 dfs，接收两个参数，分别为要比较的两个节点 left 和 right。

2. 在 dfs 函数中，首先处理基本情况： a. 若两个节点都为空，返回 true，表示它们对称。 b. 若一个节点为空，另一个节点非空，返回 false，表示它们不对称。

3. 如果两个节点都非空，判断它们的值是否相等：

   a. 若值不相等，返回 false。

   b. 若值相等，递归地比较它们的子树：将左节点的左子树与右节点的右子树进行比较，将左节点的右子树与右节点的左子树进行比较。只有两个子树比较结果都为 true 时，才返回 true。

4. 定义 isSymmetric 函数，调用 dfs 函数，并将根节点的左右子树作为参数传入。

5. 返回 dfs 函数的结果，即得到二叉树是否对称的判断。

通过递归地比较每个节点的左右子树，来判断二叉树是否对称。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return dfs(root, root);
    }
    
    bool dfs(TreeNode* p, TreeNode* q) {
        if (!p && !q) return true;
        if (!p || !q) return false;
        return p->val == q->val && dfs(p->left, q->right) && dfs(p->right, q->left);
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return dfs(root, root);
    }
    
    public boolean dfs(TreeNode p, TreeNode q) {
        if (p == null && q == null) return true;
        if (p == null || q == null) return false;
        return p.val == q.val && dfs(p.left, q.right) && dfs(p.right, q.left);
    }
}

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSymmetric(root *TreeNode) bool {
    return dfs(root, root)
}

func dfs(p, q *TreeNode) bool {
    if p == nil && q == nil {
        return true
    }
    if p == nil || q == nil {
        return false
    }
    return p.Val == q.Val && dfs(p.Left, q.Right) && dfs(p.Right, q.Left)
}

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

解题思路

这题怎么遍历都可以，只要记录一下遍历到的最深层数即可，作者比较喜欢层序遍历，直接返回遍历了多少层就行。具体操作如下：

1. 如果根节点为空，最大深度为 0。

2. 创建一个双端队列 q，将根节点加入队列。定义一个变量 depth 存储最大深度。

3. 进入循环，当队列不为空时，执行以下步骤：

   a. 获取当前队列的大小 sz，表示当前层的节点数量。

   b. 遍历当前层的所有节点，执行以下操作：

   • 取出队首节点。
   • 若当前节点的左子节点不为空，将左子节点加入队列。
   • 若当前节点的右子节点不为空，将右子节点加入队列。

   c. 完成一层节点的遍历后，将最大深度加 1。

4. 循环结束后，返回最大深度 depth。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
// 层序遍历
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (!root) {
            return 0;
        }

        queue<TreeNode*> q{{root}};
        int depth = 0;

        while (!q.empty()) {
            depth++;
            for (int i = q.size(); i > 0; i--) {
                auto node = q.front();
                q.pop();
                if (node->left) {
                    q.emplace(node->left);
                }
                if (node->right) {
                    q.emplace(node->right);
                }
            }
        }

        return depth;
    }
};

// 递归
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
// 层序遍历
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;

        while (!queue.isEmpty()) {
            int size = queue.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
        }

        return depth;
    }
}

// 递归
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

// 层序遍历
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }

    queue := []*TreeNode{root}
    depth := 0

    for len(queue) > 0 {
        size := len(queue)
        depth++
        for i := 0; i < size; i++ {
            node := queue[i]
            if node.Left != nil {
                queue = append(queue, node.Left)
            }
            if node.Right != nil {
                queue = append(queue, node.Right)
            }
        }
        queue = queue[size:]
    }

    return depth
}

// 递归
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    return max(maxDepth(root.Left), maxDepth(root.Right)) + 1
}

---

110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

解题思路

树形dp类问题，dfs问左右子树要他们的高度；然后判断一下高度差绝对值是否超过1，超过1标记false；返回左右子树高度最大值加1，最后返回标记。具体操作如下：

1. 定义一个变量 ans 初始化为 1，用于表示二叉树是否平衡。
2. 定义一个辅助函数 dfs，接收一个参数 root，用于计算节点的深度。
3. 在 dfs 函数中，处理基本情况：如果节点为空或 ans 为 0（表示已经确定二叉树不平衡），则返回 0。
4. 对当前节点的左右子节点递归调用 dfs 函数，计算左右子树的高度 leftHigh 和 rightHigh。
5. 如果左右子树高度差的绝对值大于 1，将 ans 置为 0，表示二叉树不平衡。
6. 返回当前节点的高度，即左右子树高度的较大值加 1。
7. 定义 isBalanced 函数，调用 dfs 函数，并将根节点作为参数传入。
8. 返回 ans，即得到二叉树是否平衡的判断。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = 1;
    int dfs(TreeNode* root) {
        if(root == nullptr || !ans) {
            return 0;
        }
        int leftHigh = dfs(root->left);
        int rightHigh = dfs(root->right);
        if(abs(leftHigh - rightHigh) > 1) {
            ans = 0;
        }
        return max(leftHigh, rightHigh) + 1;

    }
    bool isBalanced(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int ans = 1;
    public int dfs(TreeNode root) {
        if (root == null || ans == 0) {
            return 0;
        }
        int leftHigh = dfs(root.left);
        int rightHigh = dfs(root.right);
        if (Math.abs(leftHigh - rightHigh) > 1) {
            ans = 0;
        }
        return Math.max(leftHigh, rightHigh) + 1;
    }
    public boolean isBalanced(TreeNode root) {
        dfs(root);
        return ans == 1;
    }
}

func isBalanced(root *TreeNode) bool {
    if root == nil {
        return true
    }
    return abs(height(root.Left) - height(root.Right)) <= 1 && isBalanced(root.Left) && isBalanced(root.Right)
}

func height(root *TreeNode) int {
    if root == nil {
        return 0
    }
    return max(height(root.Left), height(root.Right)) + 1
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

func abs(x int) int {
    if x < 0 {
        return -1 * x
    }
    return x
}

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

解题思路

翻转二叉树就是递归的思路，先反转自己，再反转左子树，右子树。二叉树的常见处理方式有两种：

• 一种是先处理自己，再处理左子树右子树，基于先序遍历的方式

• 另一种一般是处理自己时候需要左右子树信息，所以就是先处理左右子树，问他们要信息，然后再处理自己，这种套路也叫树形dp，基于后序遍历的方式。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root == nullptr) return root;
        swap(root->left, root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return root;
        TreeNode left = root.left;
        root.left = root.right;
        root.right = left;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

func invertTree(root *TreeNode) *TreeNode {
    if root == nil {
        return root
    }
    root.Left, root.Right = root.Right, root.Left
    invertTree(root.Left)
    invertTree(root.Right)
    return root
}

572. 另一棵树的子树

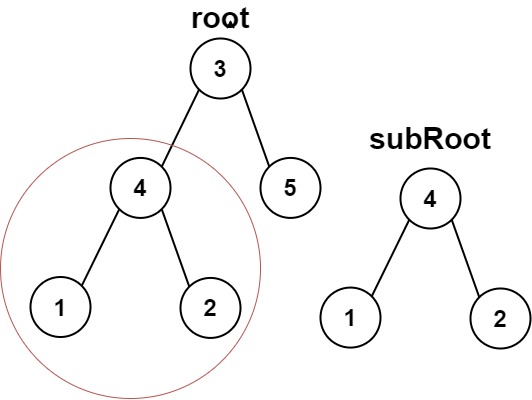
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

解题思路

其实就是递归的去检查每个节点是否相同。具体解题思路如下：

1. 定义一个辅助函数 check，接收两个参数 root 和 subRoot，用于检查两个二叉树是否相同。

2. 在 check 函数中：

3. 递归调用 isSubtree 函数，分别检查 root 的左子树和右子树是否包含 subRoot，返回它们的或（OR）操作结果。

   • 如果两个树都为空，则返回 true。
   • 如果其中一个树为空，另一个树不为空，则返回 false。
   • 如果两个树的根节点值不相等，则返回 false。
   • 递归调用 check 函数，比较两个树的左子树和右子树，返回它们的与（AND）操作结果。

4. 定义 isSubtree 函数，接收两个参数 root 和 subRoot。

5. 如果 root 为空，返回 false。

6. 调用 check 函数，检查当前 root 和 subRoot 是否相同。如果相同，返回 true。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if (root == nullptr) return false;
        if (check(root, subRoot)) return true;
        return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }

private:
    bool check(TreeNode* root, TreeNode* subRoot) {
        if (root == nullptr && subRoot == nullptr) return true;
        if (root == nullptr || subRoot == nullptr) return false;
        if (root->val != subRoot->val) return false;
        return check(root->left, subRoot->left) && check(root->right, subRoot->right);
    }
};

class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (root == null) return false;
        if (check(root, subRoot)) return true;
        return isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
    }

    private boolean check(TreeNode root, TreeNode subRoot) {
        if (root == null && subRoot == null) return true;
        if (root == null || subRoot == null) return false;
        if (root.val != subRoot.val) return false;
        return check(root.left, subRoot.left) && check(root.right, subRoot.right);
    }
}

func isSubtree(root *TreeNode, subRoot *TreeNode) bool {
    if root == nil {
        return false
    }
    if check(root, subRoot) {
        return true
    }
    return isSubtree(root.Left, subRoot) || isSubtree(root.Right, subRoot)
}

func check(root *TreeNode, subRoot *TreeNode) bool {
    if root == nil && subRoot == nil {
        return true
    }
    if root == nil || subRoot == nil {
        return false
    }
    if root.Val != subRoot.Val {
        return false
    }
    return check(root.Left, subRoot.Left) && check(root.Right, subRoot.Right)
}